This article comes from OneRaynyDay, an undergraduate student in computer science at the University of California, Los Angeles. He likes to talk about machine learning concepts in a clear, easy-to-understand and humorous way, especially the mathematical concepts. Compared to the author's "macro-geeks," Xiaobian has limited capabilities and can only do his best to calculate and verify concepts that were not introduced in the article. If the content is wrong, welcome to point out in the message.

Monte Carlo is a casino
table of Contents
Introduction
Monte Carlo action value
Getting to know Monte Carlo
Monte Carlo Control
Monte Carlo ES On-Policy:ε -Greedy Policies Off-policy:Sampling of Importance
On-Policy Model in Python
In the reinforcement learning problem, we can use the Markov decision process (MDP) and related algorithms to find the optimal action value functions q∗(s,a) and v∗(s), which are found through strategy iteration and value iteration. The best strategy.
This is a good way to solve many of the problems in stochastic dynamic systems in reinforcement learning, but it has many limitations. For example, does the real world really have so many problems that clearly know the state transition probability? Can we use MDP anytime, anywhere?
So, is there a way to both approximate the calculation of some computations that are too complicated and handle all the problems in the dynamic system?
This is what we are going to introduce today — the Monte Carlo approach.
Introduction
Monte Carlo is a well-known casino in the Principality of Monaco. It contains games such as roulette, craps, and slot machines. Similarly, the Monte Carlo method is based on random numbers and statistical probabilities.
Unlike general dynamic programming algorithms, the Monte Carlo method (MC) takes a fresh look at the problem. In short, it focuses on: How many samplings do I need to make from the environment to identify the best strategies from bad strategies?
On Smart Note: We can cite two examples of dynamic programming algorithms and MC's perspective differences:
Q: 1+1+1+1+1+1+1+1 =? Answer: (掰 finger) 8. Q: What about +1 after the above formula? Answer: 9! Q: How is it so fast? A: Because 8+1=9. ——Dynamic planning: Remember the solutions you have solved to save time!
Q: I have a circle with a radius of R and a bean. How do you calculate the pi? A: In a round coat with a 2R side square, randomly throw beans inside. Q: How do you say this? A: If you throw N beans, there are n beans that fall into the circle. The larger N is, the closer n/N is to πR2/4R2. - MC: It's completely easier to calculate by hand than ancestor Chongzhi. I'm ashamed!
In order to explain MC from a mathematical point of view, here we first introduce the concept of "return" (R), or "return", in reinforcement learning to calculate the long-term expected return (G) of an agent:
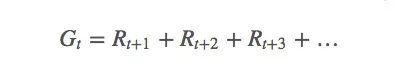
Sometimes, the state probability of the current strategy is non-zero within this episode. It is also non-zero in successive episodes. We must consider the importance of current returns and future returns.
It is not difficult to understand that the rewards of reinforcement learning tend to lag behind. For example, when you play Go, the current child may not seem useful at present, but it may show a huge advantage or disadvantage in the following situation. Therefore, our Go players need to consider long-term returns. This measure is the discount factor γ:
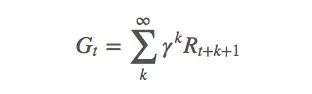
γ is generally between [0,1]. When γ = 0, only the current return is considered; when γ = 1, the current return and future returns are balanced.
With the gain Gt and the probability At, we can calculate the function value V(s) of the state s under the current strategy:
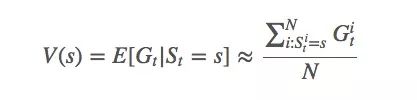
According to the law of large numbers, when N approaches ∞, we can get the exact function expectation. We index the ith simulation. It can be found that if you use MDP (which can solve 99% of the reinforcement learning problems), because it has a strong Markov nature, that is, the next state of the system is only relevant to the current state, and has nothing to do with the previous information:
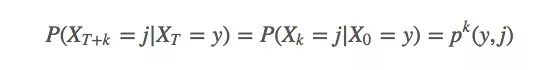
We can deduce the fact that t has nothing to do with expectations. So we can use Gs directly to represent the expected return from a certain state (when moving the state to t = 0).
Getting to know Monte Carlo
The most classic method of calculating the value function is to sample each first visit of the state s and then calculate the mean, which is the first-visit MC prediction. The following is the algorithm to find the optimal V:
Pi = init_pi()
Returns = defaultdict(list)
For i in range(NUM_ITER):
Episode = generate_episode(pi) # (1)
G = np.zeros(|S|)
Prev_reward = 0
For (state, reward) in reversed(episode):
Reward += GAMMA * prev_reward
# backing up replaces s eventually,
# so we get first-visit reward.
G[s] = reward
Prev_reward = reward
For state in STATES:
Returns[state].append(state)
V = {state: np.mean (ret) for state, ret in returns.items ()}
Another method is every-visit MC prediction, which calculates the average of all visits of s. Although the two are slightly different, in the same way, if the number of visits is large enough, they will eventually converge to similar values.
Monte Carlo action value
If we have a complete model, we only need to know the current state value and we can choose an action that can get the highest return. But what if you don't know model information? The characteristic of Monte Carlo is that he does not need to know the complete environment knowledge, but can only learn by experience. So when we don't know what state the action will lead to, or if there is interaction within the environment, we use the action value q* instead of the state value in the MDP.
This means that we estimate qπ(s,a) instead of vπ(s), and the return G[s] should also be G[s,a]. If the original G's spatial dimension is S, it now becomes S×A, which is a big space, but we still have to continue sampling it to find out the state−action pair of each state. Expected return.
As mentioned in the previous section, Monte Carlo has two methods for calculating value functions: first-visit MC and every-visit MC. Because the search space is too large, if the strategy is too greedy, we cannot traverse every state−action pair, and we cannot balance exploration and exploitation. The solution to this problem will be described in the next section.
Monte Carlo Control
Let's review the strategy iteration of MDP first:
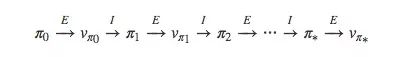
For the Monte Carlo method, its iterative method is not different from what we imagined. It starts with π, then qπ0, then π′...
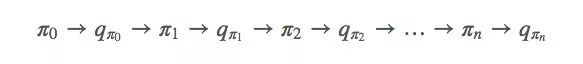
On the Smart Note: The process from π to q represents a complete strategic evaluation process, and from q to π represents a complete strategic process. The strategy evaluation process will produce a lot of episodes, and get a lot of action-value functions close to the real function. As with vπ0, although each of the motion values ​​we estimate here is an approximation, by iterating with the approximation of the value function, after many iterations, we can still converge to the optimal strategy.
Since qπ0 and vπ0 are not so different, MDP can be solved by dynamic programming. Then we can continue to apply the Bellman optimality equation, that is:
If you don't understand it, here's a Chinese introduction: Reinforcement Learning (3) - MDP's dynamic programming solution.
The following is the exploration vs. exploitation.
Monte Carlo ES
In the face of such a large search space, one remedy is to assume that each of our episodes will start from a specific state and take a specific action, namely exploring start, and then sample all possible rewards. The idea behind it is to assume that we can start from any state and take all actions at the beginning of each episode. At the same time, the strategy evaluation process can be completed with an unlimited number of episodes. This is unreasonable in many cases, but it has miraculous effects in the environment of unknown issues.
In actual operation, we only need to add the following in the previous code block:
# Before (Start at some arbitrary s_0, a_0)
Episode = generate_episode(pi)
# After (Start at some specific s, a)
episode = generate_episode (pi, s, a) # loop through s, a at every iteration.
On-Policy:ε -Greedy Strategy
So, if we can't assume that we can start with arbitrary states and take arbitrary actions? No longer greedy, there is no longer an unlimited number of episodes. Can we still fit the optimal strategy?
This is the idea of ​​On-Policy. The so-called On-Policy refers to the strategy that evaluates and optimizes the decisions that are now being made; and the off-policy improves the strategies that are different from the ones that are currently making decisions.
Because we want to "no more greed", the easiest way is to use ε-greedy: for any time t of the implementation of "exploration" small probability ε <1, we have the probability of ε will carry out the exploration, with 1-ε probability Exploitation will occur. The probability of ε-Greedy's random selection strategy (not greedy) is ε/|A(s)| compared to greedy strategies.
The question now is whether this will converge to the optimal policy π* of the Monte Carlo method? - The answer is yes, but it is only an approximation.
ε-Greedy convergence
Let's start with q and an ε-greedy strategy π'(s):
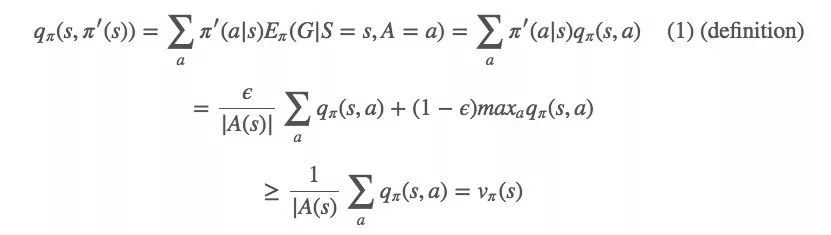
The ε-greedy strategy monotonically improves vπ like a greedy strategy. If you look back at each step, it is:
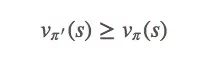
(1)
This is our goal for convergence.
This is only a theoretical result. Can it really fit? Obviously not, because the optimal strategy is fixed, and the strategy we choose is forced to be random, so it can not guarantee convergence to π * - we refactor our problem:
Suppose we do not use the probability ε to randomly select strategies, but ignore the rules and truly implement a completely random selection strategy. Then we can guarantee at least one optimal strategy. That is, if the equation in (1) is true, then we have π=π', so vπ=vπ', subject to environmental constraints, and the strategy we obtain at this time is optimal under random conditions.
Off-policy: importance sampling
Off-policy annotation
Let's start with some definitions:
Ï€: target strategy, we hope to optimize these strategies have obtained the highest return;
b: action strategy, we are using b to generate various data that will be used after π;
π(a|s)>0⟹b(a|s)>0∀a∈A: The overall concept.
The Off-policy policy usually involves multiple agents. One of the agents has been generating data that another agent is trying to optimize. We call them behavioral and target strategies respectively. Just as neural networks are more “interesting†than linear models, the Off-policy strategy is generally more fun and more powerful than the On-Policy strategy. Of course, it is also more prone to high variance and more difficult to converge.
Importance sampling is a method used in statistics to estimate the nature of a distribution. Its role here is to answer "given Eb[G], what is Eπ[G]"? In other words, how do we use the information obtained from b-sampling to determine the expected return of π?
Intuitively, if b chooses many a and π also chooses a, then b should play an important role in π; conversely, if b chooses a, π does not always follow b to a. b The state produced by a does not have an excessive effect on the state of π due to a.
The above is the basic idea of ​​importance sampling. Given a strategy iterative trajectory (Si, Ai) Ti = t from t to T, the possibility of a strategy π fitting to this trajectory is:
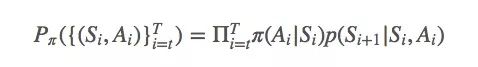
Simply put, the ratio between π and b is:
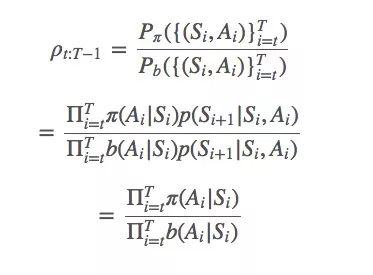
General importance sampling
Now we have many methods for calculating the optimal solution of EÏ€[G] with Ït:T−1, such as the importance importance sampling. Let us sample N episodes:
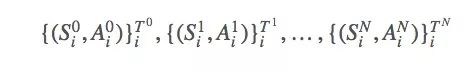
The first appearance of s is:
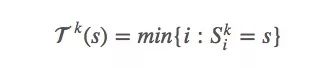
Since we want to estimate vπ(s), we can use the first-visit method mentioned earlier to calculate the mean to estimate the value function.
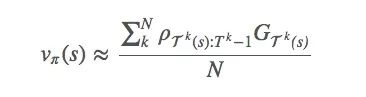
Using first-visit here is only for simplicity, and we can also extend it to every-visit. In fact, we should measure the return of each episode in combination with different methods, because if π can fit the trajectory of the optimal strategy, we should give it more weight.
This method of importance sampling is an unbiased estimate and it may have serious variance issues. Consider the importance ratio, if ÏT(s):Tk−1=1000 in an episode of the k-th round, this is too large, but it is entirely possible. How much impact does this 1000 have? If we only have one episode, its influence can be imagined, but because reinforcement learning tasks are often very long, plus there are many multiplication calculations, this ratio will have two results of explosion and disappear.
Weighted importance sampling
To reduce the variance, one possible method is to add weights to calculate the sum:
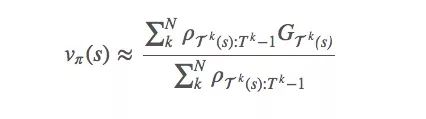
This is called weighted importance sampling. It is a biased estimate (the deviation tends to 0), but at the same time the variance is reduced. If it is practice, we strongly recommend weighting!
Incremental implementation
The Monte Carlo forecasting method can also be implemented incrementally. Assuming we use the weighted importance sample in the previous section, we can obtain some sampling algorithms in the following form:
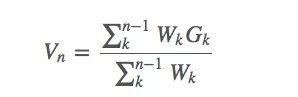
Which Wk is our weight.
Suppose we have an estimate Vn and a current return Gn, we use Vn and Gn to estimate Vn+1, and we use nkWk to represent the sum Cn of the weights of the previous rounds of returns. Then this equation is:
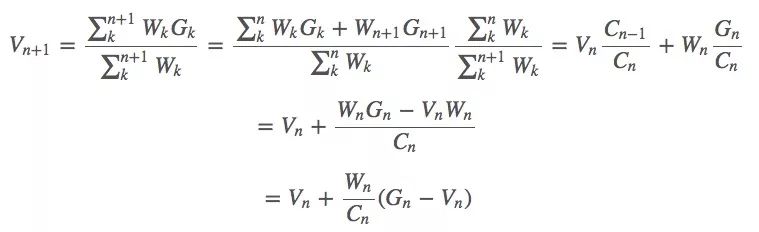
Weight: Cn+1=Cn+Wn+1
Now, this Vn is our value function, and the same method is also applicable to the action value function Qn.
While we update the price function, we can also update our strategy π - argmaxaQπ(s,a).
Note: This involves a lot of mathematics knowledge, but it is already very basic. To be exact, the most cutting-edge is also very close to this.
The following is a sample introduction for discount factors and rewards. Please refer to the original article for details.
On-Policy Model in Python
Since the Monte Carlo method code usually has a similar structure, the author has created a Monte Carlo model class that can be used directly in Python. Interested readers can find the code on Github.
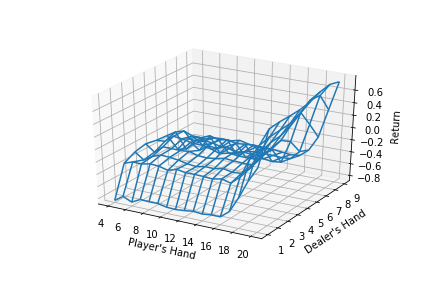
He also made an example in the original text: solve the Blackjack problem with ε -greedy policy.
In a word, the Monte Carlo method uses episode sampling to learn the best value function and the best strategy. It does not need to establish sufficient knowledge of the environment, and it is a good method worth trying when it does not meet the Markov nature. It is also a good foundation for newcomers to contact reinforcement learning.
This article refers to reading:
[1] Reinforcement Learning (II) - Markov Decision Process MDP: https://
[2] Enhanced Learning (IV) - Monte Carlo Methods: http://
[3]Algorithm-Dynamic Programming--From rookie to veteran: https://blog.csdn.net/u013309870/article/details/75193592
[4] Monte Carlo used to calculate pi: http://gohom.win/2015/10/05/mc-forPI/
[5] Monte Carlo Method: https://blog.csdn.net/coffee_cream/article/details/66972281
Golf Cart Charger,Electric Forklifts Charger,Electric Motorcycles Fast Charger,Battery Charger For Ebike
HuiZhou Superpower Technology Co.,Ltd. , https://www.spchargers.com